Home | Links | Applets | Papers | Class Plan | Team

Java Applets

Be aware that some of the applets will require you to have the Java JRE 1.4 plug-in (or higher version) on your machine. Once you install this plug-in and reboot your machine, the applets will work. If you wish to use the source code for our applets to develop your own applets, go ahead and download the full Java SDK 1.4, which includes the JRE plug-in as well.

Screenshots	Description of Applet
	CA for Squaring by Haile Eyob The java applet is based on the squaring rule. The 1DCA generates the square of integer numbers. Each cell uses only the 3 squares directly above it to determine its color. There are 5 possible color for each cell. For a given n black squares the block would produce a block of n*n red squares.
	Searching for 1D CAs by Harry Fu CAMorph is a 1-D CA Java Applet Player that displays 9 CA views at once. It runs discrete valued and continuous valued CA with user intervention. For discrete CA, there are 2 – 16 states between 1 – 3 radius. For continuous CA, it uses diffusion rule and wave equation to generate variety of patterns. Please refer to A New Kind of Science pages 55, 56, 155 – 168, 243 to experiment with different CA rules.
	1D CA Traffic Simulation by Henry Jiang I am making this site in an attempt to model the traffic flow using 1 D cellular automata. The model will follow these rules taking from Dr. Ca Hortsmann's traffic simulator applet, which follows the rules from Kai Nagel and Michael Schreckenberg. The interface at this point is near completion with minor decisions to make and features to add. With some addition features, the code will be extended to work with the new features.
	Chaoticity of *3 by Tan Ma The operations of elementary arithmetic are so simple. In here, patterns produced by starting with number 1, and then successively multiplying by factor of 3. In each case, the digit sequence of the number obtained at each step is shown in base 2. The result of mutiplication by 3 yields a much complicated pattern.
	2D Turing Vants by Christine Meyer Vants is a 2-D Turing Machine, commonly called Langston's Ant which was developed by Chris Langston. The original version moves right when the background color is black, and moves left when the background color is white. The background color reverses color when the ant moves to a new cell.
	Hexagonal CA Crystals by Gauri Nadkarni Hexagonal CA crystals is a 2-D CA snowflake java applet. This applet displays beautiful and intricate snowflake patterns on a hexagonal grid. It is based on the snowflakes described in NKS pp. 369-372. It displays the seven-sum 3-state totalistic rules. The user clicks on any grid cell to set the initial seed. A set of rules are provided. The user can play around with the rules by setting different seeds. The applet also provides with a zoom facility which resizes the hexagonal cells.
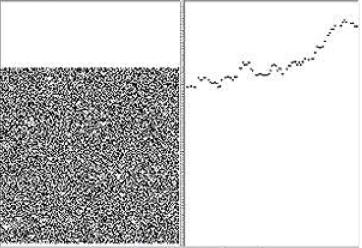
	Financial Market CA by Baohoi Nguyen This is a Financial Market CA. It recreates the randomness found in stock prices through the randomness found in CAs. The X-axis is time. The Y-axis value is determined by the differences of black (sellers) and white (buyers) cells.
	Reversible 1D CA by Kwanghyun Paek Reversibility is a universal characteristic of physical law, and it is a precondition for the second law of thermodynamics to hold. In Cellular Automata, certain basic features of the physical laws, such as uniformity and locality, are directly built in. However, reversibility does not come automatically: it has to be programmed in. Running a cellular automaton backward is possible only when the cellular automaton defined by the original rule is also backward-deterministic. In special cases a system can have the same rule for both direct and inverse rules. By using the final state of the forward run as an initial state for the backward run, the system can rebuild the backward steps. The Reversible 1D CA Applet simulates the reversible 1D cellular automata.
	CACont by Shruti Parihar CACont is a java applet implementing continuous valued Cellular Automata. Different rules like the Heat Rule, Wave Equation etc can be tried on this applet.
	2D Pattern-Forming CA by Rukman Senanayake This applet demonstrates a 2D CA which can be used to generate patterns found in biological systems, such as the stripes of a zebra or the pattern on a mollusc shell. The main parameters are the weights which one can assign to the neighboring cells. By adjusting these weights, as described by Wolfram in NKS, a multitude of patterns can be seen.
	Sound Synthesizing 1D CA by Karl Schramm CASound is a 1D continuous cellular automata with a twist. The twist being that it generates sound. How does the synthesis work? During each generation the values of the cells are used to create an audio buffer. This buffer is then played much like a typical audio file (e.g. .wav, .mp3, etc.). Thus the sound you hear is an interpretation of the values of cells themselves. So as the CA changes and progresses, the sounds you hear do as well. For more information on continuous 1D CAs, please refer to pages 155-166 in Wolfram's book.
	1-D Turing Machine Applet by Min Yang This 1-D Turing Machine applet uses time-space display to show you the outputs of running the TM rules clearly. You can choose rule from 2-state, 3-state, 4-state, 5-state Busy Beaver rules and other class 3, class 4 rules from Wolfram's book. The cell is blank when its status is "0" and turns to gray when its becomes "1". The clock hand stays in the cell which tape head locates in. It also represents the state number by turning clockwise.