Abstract
This paper compares
digital signal processors with cellular automata and explores a possible
link between the two. The emphasis of the comparison is centered on the
parallel nature of both devices.
For digital signal processing, parallelism is discussed with
regards to hardware as well as software. Additionally a brief overview
of digital signal processing is provided. Topics covered in this overview include analog to digital
signal conversion, sampling, superposition, decomposition, Fourier
transformation, sinusoidal fidelity, and linearity.
Introduction
Cellular automata (CA) have long resided in the
ethereal world of theoretical computing devices. Over the years researchers from
around the globe have developed various ways to represent these
fictional machines in both hardware as well as software. At MIT, students and researchers have
built CAM-8 [2], a multiprocessor machine designed to mimic a CA. The popular mathematical
visualization application, Mathematica, has powerful tools for creating
CAs in software [9]. Perhaps
another incarnation of CAs, a more natural one, has existed all
along. Digital signal
processing, carried out by digital signal processors, may represent a
truly natural physical manifestation of these theoretical
machines. Here we examine this
possible relationship between cellular automata and digital signal processing.
A Brief Tour of Digital Signal Processing
Digital
signal processing first came on the scene in the 1960s, shortly after
the advent of the digital computer, and is used in a broad range of
applications, including: multiplexing, signal encoding, and compression
in telecommunication systems, sound and video effects in the
entertainment industry, image compression for space exploration, radar
and sonar for military use, and medical imaging (CAT and MRI).
Digital
signal processing is typically carried out by highly specialized
microprocessors, known as digital signal processors, which perform only
a single specific signal processing task. Digital signal processors are so synonymous with the
field of digital signal processing that they are both associated with
the same acronym: DSP (To avoid confusion, from here onward we will
only refer to digital signal processors as DSPs.). With the increasing performance of
today’s personal computers, DSPs can now be simulated in software. However, there are many cases, such
as embedded systems, where a cumbersome personal computer would not
meet space, heat, or cost constraints. Additionally, digital signal
processing calculations are often required to be carried out in
realtime. Such a restriction
may be even too rigorous for today’s advanced personal computers. It is for these reasons that DSPs
are still the primary choice for digital signal processing
applications.
From
the top down view, a DSP is a fairly simple device. It receives a signal through an
input, applies a calculation to the signal, and outputs the
result. Of course, the
calculations a DSP applies to a signal can be quite complex, but how it
functions is still quite simple: new data goes in and altered data
comes out.
The
signals that are fed into a DSP begin and end their lives as continuous
analog waveforms. Thus before
a signal can be processed by a DSP it must first be converted into
digital format. A special DSP,
known as an analog to digital converter (ADC), carries out the analog
to digital conversion (A/D conversion). The counterpart to the ADC is the digital to analog
converter (DAC). As one might
expect, a DAC converts a digital signal to an analog signal (D/A
conversion).
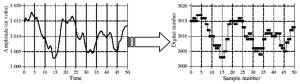
Figure 1. Conversion from an analog signal to a
digital signal (A/D conversion). [6: page 37]
An
ADC converts an analog signal into digital by taking samples of the
signal at regular intervals and outputting the results as a 1D array.
The appropriate sampling frequency is determined by Shannon’s sampling
theorem. It states that it is
necessary to sample a signal at a rate greater than double the highest
frequency component in the signal in order to retain all the frequency
components. In other words, if
a signal is sampled at a frequency less than twice the highest
frequency of the signal, it may be impossible for a DSP to accurately
reproduce the analog waveform from the sampled data. This fact, coupled with the limited
range of human hearing (20 Hz – 20 kHz) explains why CD-quality audio
is sampled at a rate of 44.1 kHz.
Once in
digital format, a signal can be passed from the ADC to other DSPs. Typically several DSPs are connected
in serial over a shared bus. Data is passed along the bus from DSP to
DSP. For instance, a typical
arrangement in audio processing would be to begin with an ADC,
following that would be a filter, after that a reverb, and finally a
DAC to output the results. Such
a chain is pictured below in Figure 2.

Figure 2. A typical DSP chain.
DSPs and Cellular Automata
There are several ways a DSP is like a cellular
automata and vice versa. Recall
the definition of a cellular automaton. A CA is comprised of a lattice of cells, arranged in any
number of dimensions (1D, 2D, 3D, etc.). Every cell contains a value. With a Discrete CA, the value is either 1 or 0. With a Continuous CA, the value can
vary over a specified range. Typically this range is normalized so that
all values lie between 0.0 and 1.0.
Each cell in the cellular lattice performs a function on the
data that is passed to it from the previous generation of cells. The
results of the function are then left behind for the next generation of
cells to process.

Figure 3. A 1D Discrete
CA and its corresponding processing rules. [9: page 32]
Using
this definition, a DSP can be viewed as a cellular automaton of sorts.
Like a CA a DSP receives data, in this case a signal, performs a
function on the data, and then outputs the results. To be more specific, it would fall
into the category of a 1D Continuous CA. The reason for this categorization is fairly
straightforward. Like a 1D
Continuous CA, a DSP receives a 1D array of data that is continuous
over a limited range. Recall
that a digitally sampled signal is simply an array of values that are
limited to the range of the sampling equipment.
There
is a problem with this analogy, however. To apply a DSP operation, say signal encoding, we
traditionally use only one DSP to perform this operation. On the other hand, a 1D CA is
comprised of an array of cells. Of course a single DSP can be
considered an array of size 1, but we need to consider that parallel
cell operation is a key element of CAs. As it turns out, there are ways of using several DSPs in
parallel to perform an operation.
We will cover this topic in greater detail shortly.
There
are other ways we can visualize symmetry between DSPs and CAs. In a serial chain of DSPs, we can
imagine each DSP in the chain as a different generation of cellular
automata. As the data is passed
from one DSP to another, it passes down successive generations of
computation. Once the data
passes the final DSP in the chain, the computation is complete. The major difference with this model
and the traditional CA is that each DSP in a serial chain may perform
different calculations. In
cellular automata the calculation remains constant throughout each
generation.
It is worth noting that a CA can also simulate a
DSP. More correctly stated, a
CA can be used to manipulate and generate signals. This can be done in at least two ways. In the first approach we divide the
range of possible cell values into subsets. Each subset is assigned a tone, typically a musical note
or a MIDI value. After an
iteration of the CA, the tones corresponding to the CA’s current state
can be played by a tone generator much like a player piano in a Western
saloon. A technique similar to this is employed by the application
CAMUS [3]. Rather than creating
tones based on cell values, CAMUS bases them on cell positions.
The
other method of generating signals from a CA is to interpret each row
as a snapshot of a waveform. The values of the cells would then be
construed as a discrete set of sample points of a signal where each
cell’s value represents the amplitude of the signal at a particular
instant. The signal is then
output to a DAC. The Java
applet CASound [5] uses this approach with a 1D Continuous CA to
synthesize sounds in realtime.
Parallelism
By their very nature cellular automata are
parallel computers. When a CA
iterates from generation to generation, every cell performs a
calculation. Of course these
calculations can be processed in a serial manner and in many CA
implementations they are. But
in theory these calculations are performed at the same time in lock
step. According to the Flynn classification,
a CA would be categorized as a SIMD (single instruction multiple
data-stream) machine. The reason for this being that the cells of a CA
are, in essence, data streams and the cells, while numerous, all
perform the same operation.
Suffice to say, parallelism is a rather important
aspect of a CA. It is this
feature that allows CAs to model particle systems such as fluid
dynamics or the growth of a crystal lattice. So if a DSP or any other system were to be compared with
a CA it must exhibit some sort of parallelism. On the surface, however, digital
signal processing is a seemingly serial task. Data is input to the DSP, a calculation is performed on
it, and the final result is then output. This notion of serial operation is further compounded by
the fact that DSPs are often linked together in a serial fashion on a
shared bus. Each DSP receives a
signal, modifies it, and then outputs the results for the next element
in the chain. While serial
operation may have occurred in early DSPs, many modern DSPs carry out
operations in parallel. Because
DSPs are often required to process data in realtime, they are highly
optimized for efficiency. Part
of this optimization is parallelization.
Data
Parallelism
Parallel
processing requires a “divide and conquer” strategy in order to be
maximally efficient. Therefore in order for a system to be
parallelizable, the data that it processes should be parallelizable as
well. For instance, a CA’s data
is typically stored in a highly compartmentalized form: namely a grid
or an array. Because a CA’s
data is so rigidly sectionalized, each cell can carry out its
calculation without altering the results of the surrounding cells.
By the
same token, the signal data used by DSPs is compartmentalized as well
because it is stored as a stream or an array. It is therefore quite parallel and well suited for many
parallel operations. For
instance, a general approach to a signal-smoothing filter is to average
the values of a data point and its surrounding neighbors. Clearly this problem is easily
parallelizable. Several DSPs
can process different parts of the signal without tampering the results
of the others. However, there
are many problems in digital signal processing that cannot be solved by
simply altering the raw digital signal data. For these problems we need a more complicated solution
that also happens to be quite parallelizable.
In
digital signal processing signals are often decomposed into smaller,
simpler signals. This
decomposition is done for several reasons. Here we outline two of them. First of all, simpler, uniform signals are easier to
process. Secondly, and most
importantly, decomposition provides a means to determine an
approximation of the equation that produced the signal. Acquiring a
signal’s equation, or an approximation thereof, is crucial for many
digital signal processing operations such as encoding or decoding data
on a carrier signal, frequency analysis, multi-band filtering, or
equalization. And as a bonus,
decomposition provides us with perfectly parallelizable data.
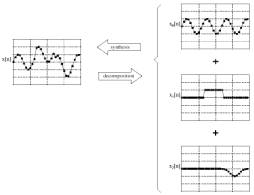
Figure 4. Signal decomposition and superposition. [6: page 98]
After
decomposition, each of these smaller, simpler signals are processed
individually. The resulting
signals are simply added together to form the final result. Thus the final signal is a
superposition of many smaller, simpler signals. Summing up the decomposed and
processed signals will only work properly if the calculations that are
applied to it are linear. Fortunately, most digital signal processing
operations are linear and those that are not can be approximated by a
linear system. A system is
linear if it has two properties: homogeneity and additivity. The homogeneity property means that
any alteration in the input signal's amplitude results in a corresponding
alteration in the output signal's amplitude. A system is considered to be additive if, for any two
inputs, the sum of the corresponding outputs is the same as if the sum
of the two inputs had been processed directly by the system.
There
are many techniques for decomposing a signal such as impulse
decomposition, step decomposition, even/odd decomposition, and
interlaced decomposition. However, Fourier decomposition remains the
most popular due to the many advantages of sine waves. Sine waves are favored
because they are uniform, easy to process, and, according to the work
of Jean Baptiste Joseph Fourier, in combination can suitably
approximate any other waveform.
But the most important property of sine waves is sinusoidal
fidelity. Sinusoidal fidelity guarantees us that if the input to a
linear system is a sine wave, the output will be a sine wave at exactly
the same frequency as the input.
In other words, if a sine wave is processed by a linear system
only a change in phase and amplitude will be seen in the resulting
signal.
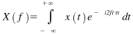
Figure 5(a). Fourier transform. Here X is the set of
frequencies, x is the set of sample points, and t is the
instantaneous moment of time.
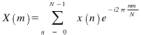
Figure 5(b). Discrete Fourier Transform (DFT). Here X is the set of frequencies
and x is the set of sample points.
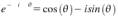
Figure 5(c). Euler’s relationship. Using this relationship we can see how a Fourier
transform decomposes a signal into sine and cosine waves.
As
we can see in Figure 5, Fourier decomposition decomposes
a signal into a several sinusoidal signals. A signal with N samples will be decomposed to N
signals, where each new signal will have N samples apiece. Half
of these N signals are cosines; the other half sine waves. Unfortunately, Fourier
decomposition is extremely computationally expensive for digital
computers because it involves integration. The technique actually utilized in digital signal
processing is the Discrete Fourier Transform (DFT), a modified Fourier
transform that deals with discrete, rather than continuous values. A DFT requires only summation rather
than integration, thus making for a more efficient and readily
parallelizable approach. It is
worth noting that most, if not all, DSPs use a modified form of the DFT
called the Fast Fourier Transform (FFT). The FFT is basically a highly optimized version of the
DFT.
Hardware
Parallelism
There are primarily two many ways in which a DSP
achieves parallelization in hardware: one internal and one
external. The internal
parallelization does not have quite as drastic an effect on the
performance of a DSP as the external one, but when dealt with the
rigorous time constraint of realtime processing, DSP designers felt it
necessary to utilize any trick they could to squeeze every possible bit
of performance out of the chips.
Internally, most modern day microprocessors are
designed with the Von Neumann architecture in mind. Many DSPs, on the other hand, are
designed with the Harvard architecture in mind. The primary difference between these
two competing architectures is that the Harvard architecture has
separate memory banks and buses for instructions and data. Since the buses and memory stores
are separate, data and instructions can be fetched in the same clock
cycle, thus bearing some limited internal parallel operation.
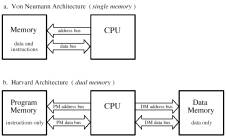
Figure 6. A comparison
of the Von Neumann and Harvard Architectures. [6: page 511]
There are architectures that improve upon the
Harvard architecture, namely Analog Devices’ Super Harvard Architecture,
or SHARC. The main improvements
SHARC designers brought about include an instruction cache and an I/O
controller. As one might
expect, a DSP algorithm spends most of its time in a loop, repeating
operations many times over. An instruction cache retains several of the
most recently requested instructions in registers within the central
processing unit (CPU), thereby reducing the number of requests to the
instruction memory bank and improving performance. The I/O controller
allows the DSP to offload any I/O operations, thus saving CPU cycles
that would normally be wasted with I/O requests.
The performance gains achieved by the Harvard
architecture and its variants are respectable, but somewhat
limited. A greater performance
boost could be achieved by linking several DSPs together to form a
multiprocessor DSP. Fortunately, this is quite possible and quite
common with DSPs. DSPs can be
arranged in both SIMD (Single Input Multiple Data stream) and MIMD
(Multiple Input Single Data stream) parallel processing
configurations. In the MIMD
configuration, each DSP operates individually, executing different
functions. In the SIMD
configuration, the DSPs perform the exact same operation on a different
subset of the signal much like the cells of a CA. With this approach, a
complete DSP operation can be performed on the entire set of data in a
single step given a sufficient number of DSPs.
When linking multiple processors together, DSP or
otherwise, a certain amount of external control logic is
necessary. Tasks such as
directing data flow and job distribution are issued by what is known as
“glue” logic. Amazingly, many
DSPs have this “glue” logic built in and are designed for multiple
processing straight out of the box. Most notable among these processors
are the aforementioned SHARC processors from Analog Devices and the
Texas Instruments TMS320.
Conclusion
Though DSPs do not make for an idyllic CA, there
is a strong resemblance. Most
notable of these common characteristics is their use of
parallelism. As we know, CAs
are the perfect SIMD multiprocessor machine. However, CAs are purely theoretical. We also know that DSPs can be, and
often are, arranged in SIMD multiprocessor arrangements. Thus making them quite the natural
multiprocessor machines and a natural cellular automaton
incarnate. A marriage of the
abstract and real seems to be a perfect fit. And perhaps it is.
In
August of 2002, IBM, Sony, and Toshiba announced that they are
developing a new massively parallel microprocessor technology. The technology, dubbed “Cell”,
features anywhere from 4 to 16 general-purpose processor cores, known
as “cells”, on one chip. These
“cells” communicate with each other via a high-speed communication bus
that is embedded within the chip. Devices utilizing a “Cell” chip can
be connected together over a high-speed network to perform distributed
computing tasks. Sony’s next
home video gaming console, the Playstation 3, is rumored to be the
first device to use “Cell” technology.
Sony’s plans for the “Cell” chip are reported to include
processing streaming multimedia data over a network so that multiple
users can play games over broad distances [7]. Cells, processing
streaming media, and massive parallelism: this sounds terribly
familiar. DSPs, CAs, and
parallelism may be set to invade the home if Sony’s plans come to
fruition. Perhaps then we can
see just how perfect this match may be.
References
[1] Lyons,
R. (2001). Understanding Digital Signal
Processing.
Upper Saddle River, NJ:
Prentice Hall.
[2] Margolus, N. (1993). “CAM-8: A Computer Architecture Based on Cellular
Automata”.
Cambridge,
MA: MIT Laboratory of Computer Science.
Available: http://www.ai.mit.edu/people/nhm/cam8.pdf
[3] Miranda,
E. (2002). “CAMUS: A Cellular Automata Music
Generator”.
Available: http://website.lineone.net/~edandalex/camus.htm
[4] Rorabaugh,
C. (1998). DSP Primer.
New York: McGraw-Hill.
[5] Schramm,
K. (2003). “CASound: Sound Synthesizing 1D CA”.
Available: http://sjsu.rudyrucker.com/~karl.schramm/applet/
[6] Smith, S. (1997). The Scientist and Engineer's Guide to Digital Signal Processing.
San Diego, CA: California
Technical Publishing.
[7] Spooner,
J., (August 6, 2002). “Chip trio allows glimpse into
‘Cell’”.
CNET News.com
Available: http://news.com.com/2100-1001-948493.html?tag=fd_top
[8] Wilkinson, B. & Allen,
M. (1998). Parallel Programming: Techniques and
Applications Using Networked Workstations and Parallel Computers.
Upper Saddle River, NJ:
Prentice Hall.
[9] Wolfram,
S. (2001). A New Kind of
Science.
Champaign, IL: Wolfram
Media, Inc.
Presentation
Slides
|