|
2D Pattern
forming Cellular Automata |
|
Table of Contents
|
|
|
Page |
|
I.
|
Introduction |
1 |
|
II.
|
Suitability of Using CA for Modeling Ecological Systems |
2 |
|
III.
|
History of Ecological Systems Modeling |
4 |
|
IV.
|
A Simple Example of an Ecological Model based on
Cellular Automata |
5 |
|
V.
|
Types of Ecological Systems Which are Frequently Modeled
using CA |
6 |
|
VI.
|
Modeling Spatial Competition in Ecological Systems using
CA |
8 |
|
VII.
|
Modeling Invasive or Spreading Behavior using Cellular
Automata |
9 |
|
VIII.
|
Modeling Gap Dynamics Using Cellular Automata |
12 |
|
IX.
|
Techniques for Improving the Effectiveness of Cellular
Automata in Ecosystem Simulations |
14 |
|
X.
|
Conclusion |
15 |
Modeling Ecological Systems using Cellular Automata
Introduction
This paper is an
attempt to explore the possible research avenues within the
field of Ecology Modeling using Cellular Automata (CA) as
the basis for the model, and to study past and present work
carried out within this framework.
Ecological systems are
generally considered among the most complex because they are
characterized by a large number of diverse components,
nonlinear interactions, scale multiplicity, and spatial
heterogeneity [Wolfram-2002], [Elsevier-2003].
Due to
this reason a simple rule-based model, such as a cellular
automata model, can be utilized to approach large-scale
problems. In CA models, each particular cell is affected by
its neighbors in a simple, rule-based manner. CA models form
a holistic class of models where space, time and states are
discrete. Because CA models are rule, rather than equation
based, they allow for the direct consideration of knowledge
that is not necessarily restricted to hard data and are
particularly useful in consideration of complex systems
[Wolfram-1986]. Therefore, CA theory allows for the modeling
of simple interactions between organisms through time.
One
interesting point to note here is that according to Wolfram
[Wolfram-2002] this complexity evident in every ecological
system is not a result of adaptation or natural selection,
but the result of simple underlying rules in such systems.
This suggestion is discussed by Wolfram [Wolfram-2002] using
3 common occurrences; namely growth of plants, biological
pigmentation patterns and growth of mollusk shells.
Suitability of Using CA for Modeling Ecological Systems
A
significant amount of research has already been done in
modeling ecological systems using cellular automata as the
primary tool, as seen by [Hrab-1995], [Gron-1998],
[Sten-1995]. Empirical studies by Wolfram and others show
that even the simple linear automata behave in ways
reminiscent of complex ecological systems. This can be seen
by the fact that the fate of any cellular automata,
irrespective of its initial configuration, will be one of
the following:
I.
To die out
II.
Become stable or cycle with a fixed period
III.
To grow indefinitely at a fixed speed
IV.
To grow and contract irregularly
And thus it can be
argued that CA are ideally suited for the purpose of
modeling ecological systems.
One other factor which
makes CA a promising candidate for this kind of research is
the fact that there is considerable controversy in the field
of ecological modeling regarding the suitability of
mathematical models for such a complex task. The hypothesis
that there is sufficient low-dimensional order to allow
prediction of ecological dynamics has been covered in
controversy for nearly a century. But during the last few
decades hypothesis such as ‘population fluctuations are
shaped largely by low-dimensional deterministic forces’ has
been rigorously and successfully tested. Resulting in the
identification of the low-dimensional deterministic
phenomena such as equilibria, bifurcations, multiple
attractors, resonance, basins of attraction, saddle
influences, stable and unstable manifolds, transient
phenomena and even chaos [Brauer-2001]. Cellular automata
have been introduced into the arena of ecological modeling
in such an environment.
CA models have been used to model a vast array of ecological
systems. They have been used to study such diverse subjects
as interactions between sea stars and coral reef
(crown-of-thorns outbreaks) and disease spread in human
populations. Although the rules used within these CA models
may be quite simple, studies carried out by Hogeweg and
Phipps show that the results are often highly dynamic.
Recent research using CA models to model large scale
phenomena has been successfully achieved. Examples for such
systems would be sub-alpine forest wave regeneration and
forest gap-phase dynamics.
History of Ecological Systems Modeling
The classical approach to modeling ecological systems is
characterized by mathematical tractability and determinism.
Labeled as the Newtonian Mechanics approach, it was first
adopted by population ecologists, and remains very much
alive as a legacy of the ‘Golden Age’ of theoretical ecology
from 1920s and 1940s. One of the shortcomings of this
approach is that it can handle only cases where a small
number of components are involved and hence chosen to deal
with ‘organized simplicity’.
The statistical mechanics approach, on the other hand, is
effective for tackling the ‘disorganized complexity’,
characterizing systems with a large number of components
that each behave more or less randomly. Ecologists are often
confronted with the so called ‘medium-number’ systems that
exhibit the ‘organized complexity’, which is the subject of
systems science. No wonder that, as systems science emerged
in the 1950s and 1960s, ecologists were among the most
active, applying and contributing to the three major
theories in systems science: general systems theory,
cybernetics, and information theory.
However, the enthusiasm for systems ecology faded away
quietly (notably in North America) during the 1980s in the
wake of the failure of several large, monolithic computer
models produced by the International Biological Program and
with the increasing recognition of the importance of
ubiquitous spatial heterogeneity and scale. While the
systems modeling approach continued to be dominant in
modeling energy flow and matter cycling of various
ecosystems, spatial modeling approaches, including
diffusion-reaction, patch (or gap) dynamics, cellular
automata, and fractal models, seemed to take over the
central place in ecological modeling during much of the
1980s and the 1990s.
A
Simple Example of an Ecological Model based on Cellular
Automata
Consider a CA where the landscape of a forest is modeled by
a fixed array where each cell in the array represents a unit
of land surface. The states associated with each cell
correspond to ecological characteristics. Using transition
rules we can model processes that involve movement through
space (e.g. fire, dispersal) in a "natural" fashion.
To see how easily the cellular automaton model can be
brought to bear on real systems, consider a system whose
states are of the form (s,t), where t denotes
"time since fire burned out the cell" and s takes one
of the values: "bare earth" (E), "grass" (G), "woodland"
(W), and "closed forest" (F). Define state transitions rules
as follows:
(E, 0) -> (G, 1),
(G, 4) -> (W, 5),
(W,49) -> (F, 50),
(s, t) -> (E, 0), if a fire ignites nearby
-> (s,t+1), otherwise
Starting
with an arbitrary "landscape", consisting of a 2-D grid of
cells in random states, the rules quickly produce patterns.
For instance, "forest zones" quickly develop, even though
the model contains no assumptions about the environment or
site preferences of the vegetation. Admittedly, this model
is a mere caricature of true forest succession, but it is
only a short jump to management models taking (say)
satellite data as inputs [Green-1993].
Since cellular automata are based on homogeneous cells this
approach can be incorporated with both pixel-based satellite
imagery and with quadrat-based field observations without
too much difficulty.
Types
of Ecological Systems Which are Frequently Modeled using CA
Space and time have always been recognized as crucial
components of ecological change. Important spatial patterns
such as aggregated distributions of plant community species
(at one or more scales) and juxtaposed neighborhood
competition, has led to continued study of vegetation
utilizing spatial methodologies [Silvertown-1992].
Population processes such as reproduction and interspecies
competition are affected by the initial spatial arrangement
of a species. The manner in which a species evolve in a
landscape is influenced by the spatial and temporal
correlations that exist in its agents.
According to [Baltzer-1998] the incorporation of spatially
explicit models in the arena of ecological modeling are
“expected to increase our ability to accurately model
populations subject to complex processes”. The inclusion of
space in vegetation models introduces more complex rules
into a simulation than those created from simple parameters.
This can lead to unpredictable chaotic simulation and
non-linear dynamics [Silvertown-1992].
The theories regarding the spatial arrangements that many
population models are based on were first introduced by
Skellam. Skellam introduced a mathematical model that can
be used to simulate population dispersal. This model is
based on the assumption of randomly distributing a species
in space, and with an associated constant growth rate.
Due to these factors we can identify three types of behavior
in ecological systems usually modeled using CA, and they
are:
-
Spatial Competition
-
Invasive or Spreading Behavior
-
Gap Dynamics
Within this paper an example of each type of ecological
model will be discussed. And how these techniques can be
improved and emerging techniques of improving these
mechanisms will also be discussed.
Modeling Spatial Competition in Ecological Systems using CA
Plants and
other organisms must secure space in order to obtain access
to scarce resources. When competing organisms are of
similar stature, competition primarily occurs between
immediate neighbors and is local to the boundaries between
the two species. According to [Silvertown-1992] the
recognition of importance of neighborhood competition in
plant populations has led to the development of many
interspecific neighborhood models for competition. And
models have been developed to analyze individual performance
in population dynamics as well as effects of spatial
patterns affect the process of competition.
One
important point to note here is that modeling spatial
competition using CA draws increased scrutiny to initial
conditions and their effect and influence on the outcome of
interspecific competition. The term “Interspecific
competition” is used to refer to the competition between two
or more species for some specific limiting resource(s),
such as sun light.
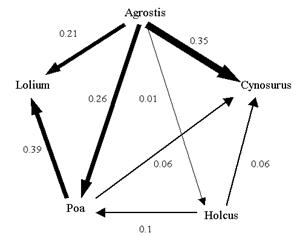 Silvertown
[Silvertown-1992] developed an experimental study using five
grass species where the following relationship was found.
Based on this a CA model was developed to analyze the
invasion process if two grass species were grown adjacent to
each other. Within this model each cell in the CA can be
one of many states, and such a state would typically
represent vacant space or occupancy by a particular
species. A probabilistic approach was used to determine the
local rules for cells which govern state transitions.
Silvertown
[Silvertown-1992] developed an experimental study using five
grass species where the following relationship was found.
Based on this a CA model was developed to analyze the
invasion process if two grass species were grown adjacent to
each other. Within this model each cell in the CA can be
one of many states, and such a state would typically
represent vacant space or occupancy by a particular
species. A probabilistic approach was used to determine the
local rules for cells which govern state transitions.
When
random initial starting conditions were used it was noted
that the extinction of the inferior competitors (Lolium, Poa
and Cynosurus) was very rapid. In aggregated models the
inferior competitors survived for much longer periods of
time. These observations are compatible with other
ecological models developed using traditional approaches.
The fact that the inferior species became rapidly extinct
suggests that aggregation (clumping) has a dramatic effect
on the rate at which stronger species can eliminate weaker
species. This introduces new factors into the arena of
spatial competition, namely configuration of patches and
juxtaposition of species. These factors seem to demonstrate
strong effects on community composition in the medium term
[Silvertown-1992].
Modeling
Invasive or Spreading Behavior using Cellular Automata
In this section we present an ecological model which has a
Geographic Information System (GIS) implementation of
cellular automata demonstrating the spread for the invasive
plant species Rhamnus alaternus [Vivienne-1999].
A Geographic Information System (GIS) is a computer program
for storing, retrieving, analyzing, and displaying
cartographic data. A GIS typically is a sophisticated
implementation specifically targeted towards deriving
interpretations from geographic data. For example, in town
planning a GIS can be used to analyze the town’s traffic
patterns and other factors to determine which is the ideal
location for a new supermarket.
According to [Vivienne-1999] GIS have been increasingly
utilized within modeling projects this decade. The primary
advantage of incorporating GIS into ecological modeling has
been integration of environmental and biological features
across a diverse set of spatial scales within a complex
terrain and heterogeneous landscape.
In this case CA are very suitable as a modeling tool because
they very effectively deal with the issue of spatial auto
correlated parameters and have - by GIS standards - better
temporal capabilities. In cases such as this where CA are
coupled with simulation systems they are very suited to the
manipulation of the ecological parameters due to their
bottom-up approach. This is analogues to the scaling from
individual to community level in this type of research.
The coupling of the CA to a GIS is done via the rule base of
the GIS. The rules for dispersal and other temporal
dynamics for the particular species are obtained from the
GIS at runtime based on the spatial and temporal data for a
particular cell. The GIS also governs some aspects of the
simulation which require long distance interactions, such as
seed dispersal by birds over coastal (geographic) barriers,
since the underlying CA is not very suited for such a task.
One of the major difficulties in this kind of simulation is
the run time complexities, to avoid extremely high run times
in this approach two layers of grids are used, one coarse
grid which is primarily updated and maintained by the GIS in
which long range interactions take place and a fine grid in
which the active spread and dispersal takes place. For
example if a long range interaction such as a seed dispersal
by a bird occurs this will be simulated by the GIS on the
coarse grid and once the location of the destination is
identified a fine grid is created for this particular locale
so that the active spreading mechanism can take place, which
is based on the CA. When the border of a fine grid is
reached the adjacent coarse grid cell is opened and
subdivided into a suitable number to form the a new fine
grid and merged with the initial fine grid. This allows the
system to handle a higher degree of complexity by focusing
on the areas of the simulation (governed by the GIS) within
which the CA must operate, without exhaustively running a CA
throughout the complete heterogeneous landscape.
The spread of the species Rhamnus alateirnus is
defined by its neighborhood or the maximum distance between
male/female plants for successful pollination. The flexible
manner in which the CA allows the manipulation of parameters
allowed the researchers to study a multitude of initial
conditions and their effects on the invasive spread of this
species. Species invasion is a good example of a complex
and not well understood problem in the area of dynamic
spatial modeling. It is also an example of complexity that
can be difficult to recreate within the limits of current
GIS technologies [Vivienne-1999]. By coupling CA with a GIS
the researchers in this case managed to overcome two key
weaknesses in both techniques.
Modeling Gap Dynamics Using Cellular Automata
In this section we will study the usage of CA to model gap
dynamics in ecological systems. Gap dynamics is extremely
important in certain ecosystems. For example in the case of
a rain forest gap dynamics play a crucial role in
maintaining tree diversity [Hubbel-1986].
When a tree dies in a closed-canopy forest, an area in which
a light filters to lower levels become accessible. As a
consequence of the sharp change in local environmental
conditions (humidity, temperature, light), trees at the gap
boundary (the edge of the newly opened gap) have a higher
mortality rate. Such ‘canopy’ disturbances, of different
intensity, are responsible for allowing other species to
grow. The whole set of gap sites at different successive
stages is believed to contain more species per tree than in
closed-canopy gap sites which have the same area. Also
openings in the canopy are believed to initiate strong
dynamic patterns in such systems. Some researchers have
shown that data obtained from the Barro-Colorado Island (BCI)
rainforest in Panama displays a fractal distribution of gaps
over space. It was shown that the BCI plot is in fact a
fractal set with a box counting dimension of 1.85. Typically
fractal structures appear in time and space as a result of
strong self-organized large-scale correlations
[Alonso-1999].
Cellular automata have been used in many instances to
demonstrate gap dynamics in ecosystems. In this section we
present a Forest Simulator which uses a Cellular Automata as
the modeling tool which tries to analyze the effects of gap
dynamics on a rain forest. The DivGame simulator
[Alonso-1999] is a oversimplified simulator for rain forest
dynamics where species diversity is taken into account (i.e.
it is not a single species model such as ForestGame
simulator). The CA used for the DivGame simulator is a
stochastic CA (there are some complications regarding the
design of the CA but these will be ignored for brevity).
In the CA model a gap is defined by a free cell. When a
tree dies, it creates gap in the canopy. Every tree death is
the starting point for a disturbance in the system. Trees at
the edge of a gap in the canopy have an increased
probability of dying. This field observation is built into
in the DivGame model using some external dynamics. When an
opening is formed as a consequence of a single tree death,
the relative environmental change of every neighboring point
at the edge of the gap is computed by the CA. One of the
primary observations the authors make based on the output of
the CA is that random disturbances can travel vast distances
within the system depending on the local neighborhood of the
area in which the disturbance took place.. The other key
observation is that two similar species are able to perform
very different walks (dispersion patterns), indicating that
for a species its assemblage (grouping) is a very path
dependent, unpredictable process.
Techniques for Improving the Effectiveness of Cellular
Automata in Ecosystem Simulations
If Cellular Automata are used for the modeling of a species
dispersion in a given landscape, then the given landscape is
divided into a lattice of homogeneous cells. One of the
primary characteristics (as mentioned earlier) of CAs are
that they are discrete in time and space. Furthermore these
cells are updated synchronously, i. e., they change their
states at the same time and in discrete time steps called
time phases. This is done with respect to their own state as
well as to those of the neighboring cells (dependent upon a
given rule). While the local evolving demonstrated by a
system can easily be described by a cellular automaton,
problems arise when individual organisms try to disperse in
space within one time phase of the system such that they
have to diffuse through several cells.
Due to the restrictions of this diffusion model researchers
have been looking for a more general solution for this
problem. Thus, it should be possible to model several
changes of cell states within one time phase of the system
without synchronization of the cells. This can be done by
describing the cell's behavior with respect to reactions to
events. A well-known technique for the description of a
technical system with event-based, concurrent, asynchronous
state changes is the modeling with Petri nets. They build
formal models that allow simulating systems where parts can
evolve without synchronization with the rest of the system
[Veronika-1998].
Another technique researchers use in this research culture
is to couple Cellular Automata with Geographic Information
Systems. This allows them to circumvent issues with
dispersion and synchronization, but maintain the CAs
superior characteristics.
Conclusions
It is clear that Cellular Automata offers many features
which make them attractive models for ecosystem
simulations. In addition to this one key factor that favors
the choice of cellular automata as the tool for modeling is
the natural complexity of ecosystems. Due to that fact that
cellular automata are descrete temporally and spatially,
there can be certain drawbacks as well, especially when it
comes to the areas of dispersion and asynchronous updating.
But these drawbacks can be effectively handled by
incorporating techniques such as Petri nets and geographic
information systems. The popularity of cellular automata as
a possible modeling tool for ecosystem simulations has been
steadily rising, and will most likely continue to grow due
to the fact that it is a simple technique which can generate
highly complex behavior.
References:
[Wolfram-2002] : Wolram, Stephan – A
New Kind of Science
[Elsevier-2003] : www.elsevier.com/locate/ecolmodel
[Brauer-2001] : Fred Brauer and Carlos
Castillo-Chavez - Mathematical Models in Population Biology
and Epidemiology
[Green-1993]: David G. Green – An
Introduction to Cellular Automata
[Silvertown-1992]: Jonathan Silverton,
Senino Holtier, Pam Dale – Cellular Automata Models for
Interspecific Competition for Space – The effect of Pattern
on Process
[Vivienne-1999]: Vivienne Cole, Jochen Albrecht - Exploring
Geographic Parameter Space With A GIS Implementation Of
Cellular Automata
[Hubbell-1986]: Hubbell, S. P. and Foster, R. B. - Biology,
chance and history and the structure of tropical tree
communities.
[Alonso-1999]: David Alonso, Ricard V. Slo’e - The
DivGame Simulator: A Stochastic Cellular Automata Model of
Rainforest Dynamics
[Veronika-1998]: Eva Veronika R´acz, J´anos Karsai -
Computer Simulations On Cellular Automata Models Of
Metapopulations In Conservation Biology