Home | Links | Applets | Papers | Class Plan | Team

Research Paper Outline

I.                    Introduction

       The development of organism is a remarkable process. Each animal or plant begin as a single cell and eventually become a mature one through a series of interrelated physical and chemical processes. A mature animal body may contain billions, trillions cells with hundreds different types/functions. Furthermore, the coat patterns of zebras are similar but really different from each other. The genes play an important role in the developing processes. But we cannot just say that the genes create the form and let it go at that. The genes can only influence development through their effects on chemical reactions, and they themselves have to be turned on and off at appropriate times. So the most important things we have to understand are the physical and chemical reactions, especially in the early stage of development. That is because once a pattern is established; it can serve as the basis for the next stage, and so on.

In 1952, Alan Turing published a paper, The Chemical Basis of Morphogenesis, using partial differential equations to explain how patterns might grow from homogeneous situation and how diffusion of morphogenetic chemicals in the animals' skins during the growth of embryo could drive instability. He considered a "ring" of identical cells containing various chemical substances, called morphogens, and the patterns result from interactions between these morphogens (Activator and Inhibitor) that diffuse in the medium and enter into chemical reactions with each other. This model is very much like a cellular automaton. In 1984, D. A. Young proposed to use Cellular Automata to simulate the reaction-diffusion models. He considered the cells lay out on a grid with two states: pigmented or not pigmented. The pigmented cell is assumed to produce a specified amount of activator and a specified amount of inhibitor that diffused at different rates across the grid. The status of each cell changes over time depending on the rules which take into account of itself and its neighbors. Young's results are similar to those obtained using continuous reaction-diffusion equations.

II.                 Alan Turing's Reaction-Diffusion Theory

1.                 Model of Embryo

       In the Chemical Basis of Morphogenesis, Turing created a model of the growing embryo. He has envisaged the idealized and simplified model of the embryo. "The model takes two slightly different forms. In one of them, the cell theory is recognized but the cells are idealised into geometrical points. In the other, the matter of the organisms is imagined as continuously distributed. The cells are not, however, completely ignored, for various physical and physico-chemical characterizations for the matter as a whole are assumed to have values appropriate to the cellular matter." In these statements we will see the tissue mass as a whole determines of differentiation and not the individual cells. We can also see the importance of gene-controlled substances. He thought every "state of the system" is to be determined from the previous state and every state consists two parts, the mechanical and chemical parts. Turing realized the chemical aspect is more important and interesting in the embryo developing process since "the characteristic action of genes is presumably chemical". To simplify his mathematical model, he only considered the state's chemical part, such as the chemical composition of each separate cell; the diffusibility of each substance between each two adjacent cells, and etc. Turing introduced the model as a continuous ring of tissue. Each ring contains N cells. It just likes the 2-D cellular automata.

In his model, there is a fix size tissue consists certain chemical substances, morphogens. The morphogens are reacting chemically with in the tissue. And at the same time they are diffusing through the tissue. In this tissue, to determine the change in cells due to diffusion, we need to know the amounts of the same morphogen in the cell and its neighbors, and the diffusion coefficient for that morphogen. If we want to find the change in cells due to chemical reaction, we have to know the concentrations of all morphogens in the one cell at that moment. It is like the cellular automaton, which also compute all cells simultaneously and each cell's status is decided by its neighbors and itself.

2.                 The Breakdown of Symmetry and Homogeneity

       How the initial homogeneous distribution of metabolites in an embryonic region can be drift into instability? Turing indicated the instability maybe triggered by random disturbances from the enviorment. The small random change may break down symmetry and homogeneity of the system. Some deviations from symmetry or homogeneity in a reaction system may be very important in the process of differentiation. The system maybe reach a state of instability in which the irregularities. If that occurs, a new and stable equilibrium will be reached. But the new equilibrium will be different from the original one.

Turing used partial differecial equations to explain the model. When a bifurcation parameter of a system passes through a certain critical value, there can be a qualitative change in behavior as a previously stable state becomes unstable. Turing used this idea to construct a system of simple partial differential equations that can be supposed to govern the concentration of some chemical substances. He showed us initial homogeneous distribution can be drifted into instability and a small displacement from the equilibrium value/condition will cause the breakdown of homogeneous.

III.               Other Scientists' Further Research

1.                 The Simulation with Cellular Automata

       The pattern formation is very difficult to predict. Computer simulation is a useful way to simulate its behavior for better understanding how the system works. Young first introduced cellular automata to simulate Turing's model in animal coat pattern. Typically, the components/cells of the system are arranged on a two-dimensional grid. Each cell is characterized by its location on the grid and its state, 'on' or 'off'. Each 'on' cell is assumed to produce a specified amount of activator and a specified amount of inhibitor that diffuse at different rates across the grid. In the simulation, each 'on' cell is represented as black and each 'off' cell is represented as white. At each time step, the program calculated the net amount of activation at each site on the grid. This is determined as the difference between the sum of all the activation from the cells in the neighborhood and the sum of all the inhibition from those cells in the neighborhood. If this total is greater than a threshold level, then the cell at that site is assigned to 'on'. Otherwise, it's assigned to 'off'. In this manner, cells switch from one state to another according to a single rule.

Wolfram (2002) believes the biological pigmentation patterns are generated by processes whose basic rules are very simple. But the basic rules are also randomly chosen. The animal coat pattern, the different shapes of leaves, the pigmentation patterns on mollusk shells, as well as many other examples of complexity and similarity in biological organisms can all be explained by computation and simple rules. And cellular automata is the best way to implement it.

2.                 The Activator-Inhibitor Scheme

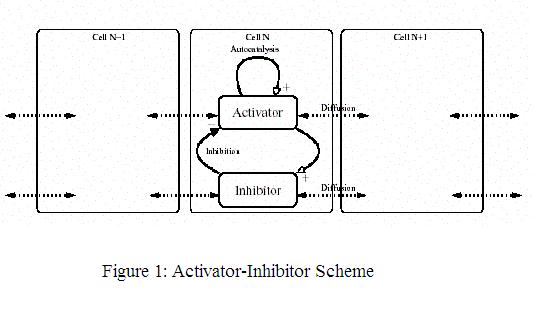
       The scheme of a biochemically feasible realization of the activator-inhibitor scheme is shown in Figure 1. A short-range substance, the activator, promotes it own production as well as that of its rapidly diffusing antagonist, the inhibitor. The concentrations of both substances can be in a steady state. A general increase in the activator is compensated by an increase in the inhibitor concentration. However, such equilibrium is locally unstable. Any local increase of the activator will increase further due to autocatalysis despite the fact that a surplus of inhibitor is also produced by this local increase. It diffuses rapidly into the surroundings and slows down the autocatalysis while the local activator elevation increases further. The crucial condition for pattern formation is that the diffusion of the inhibitor is much higher than that of the activator. Meinhardt (1995) pointed out that "relatively simple molecular interactions based on local self-enhancement and long range inhibition allows the formation of stable patterns".

IV.              Conclusion

       After reading Turing and other scientists' paper, we can see Turing's model of embryo is really a cellular automaton which rans simple rules, but cause unstable results. His research opened a new world to think of biological pattern formation for both mathematicians and biological scientists.

V.              Bibliography

[1]      Turing, A. M., "the Chemical Basis of Morphogenesis", Philosophical Transactions of the Royal Society of London. Series B, vol. 237, pp. 37-72, Aug. 1952

[2]      Jean,Roger, "Mathematical Approach to Pattern and Form in Plant Growth", John Wiley & Sons, Inc., 1988

[3]      Young, D. A. "A Local Activator-Inhibitor Model of Vertebrate Skin Patterns. Mathematical Biosciences", 72, pp. 51-58, 1984

[4]      Meinhardt, H., "the Algorithmic Beauty of Sea Shells", Springer-Verlag Berlin Heidelberg 1995

[5]      Prusinkiewicz, P., Modeling and Visualization of Biological Structures, Proceeding of Graphics Interface '93 Toronto, Ontario, pp 128-137, 1993

[6]      Walter, M., Fournier, A., Reimers, M., "Clonal Mosaic Model for the Synthesis of Mammalian Coat Patterns"

[7]      Sandberg, A., "Models of Development"