1
Introduction
Modern day
science is unable to describe an entire universe that
scientists might want to study. While the most
sophisticated mathematic formula and physics law only
explain some of the concepts that models part of this
ever expanding universe, scientist are constantly
looking for simple, yet comprehensive model to describe
what human perceive. Finding a universal model that
explains the entire universe can be challenging. The
concept of emergence, for instance, consists of
irreducibility and unpredictability properties that
prevent scientists from concluding this finding. In A
New Kind of Science, Wolfram stated in Principle of
Computational Equivalence that asserts essentially, any
process that is not obviously simple would equivalent in
its computational sophistication [7]. It implies
complicated processes that are not obviously
understandable will be computationally irreducible. In
spite of many processes in this universe with behavior
that can be described with mathematic formulas or
physics laws, there are unpredictable behaviors
emerging, as one perceive in everyday experience. How to
predict behavior using concise mathematic formulas or
physics laws for a system becomes a consensus for
science arenas. Nevertheless, how to explain a complex
system behavior with a simple model becomes wonder for
scientists. A cellular automaton model has been used to
simulate life and artificial life. Some behaviors that
emerged in cellular automata systems seemed random and
highly unpredictable. For example, how do we determine
if one cellular automaton rule indeed belongs to a
certain class? Perhaps there is not sufficient time
lapse for such an observation. One might argue that if
we keep on observing every step of evolution for a
particular cellular automaton experiment, ultimately, it
must show a result. In fact, watching every single step
of evolution and hoping to obtain an outcome turns out
to be impractical. There have been numerous mathematic
formulas and physics laws modeled as a foundation to
explain matters we experience and perceive in this
universe. Many of these formulas or laws appear
complicated, and others may seem incomprehensible. This
led to the notion that no such simple model can ever
describe everything in the universe. Through using
cellular automata as a model for science exploration, we
can analyze how these concepts emerge in emergent
computing where property such as irreducibility and
unpredictability exist. Consequently, these properties
prevented us from perceiving and analyzing models that
describe nature.
2 Using CA as Model for Nature
Why is Cellular Automata
used as a model to elaborate these emergence properties
in nature? Cellular automaton has been studied and
modeled as one of the prime experiments for emergent
computing [1]. It involved using a large number of cells
that interconnected to form arrays. These arrays of
cells update synchronously in parallel that resembles
some properties of the physical world. Knowing its
parallelism and evolutionary progression, cellular
automaton can be viewed as a progress of events moving
through space and time. Since cellular automata rules
are given as initial condition for further evolution, it
leads to notion that irreducibility and unpredictability
are produced intrinsically. Yet, these properties still
exist in nature even if the universe is likely to be
running with simple rules.
According to Wolfram, the
universe is likely to be running with certain simple
rules. These simple rules may in fact produce some
behaviors that are computationally irreducible, which
lead to unpredictability. This phenomenon emerged in
many parts of nature. Cellular automata model presents
some of these phenomena in respect. If we model the
universe with a computation of running a simple rule,
will the simple rule illustrate every aspect of our
nature? Alternatively, nature is operating at the level
of phenomena that cannot be described by human
perception. Despite these unknown controversies,
irreducibility and unpredictability inevitably emerge in
every scale of our nature.
3 Irreducibility
3.1 Cohesive Relation
Collier uses concept of
cohesion to explain why there is a property of
irreducibility in nature. According to Collier, cohesion
can account for irreducibility. The basic criterion for
natural physical objects depended on continuity of space
and time. This also resembles the intuition that natural
physical objects move together through space and time.
Cohesion represents those factors that causally connect
the components of its matters through space and time
[2]. It manifests this stability for objects in its
underlying property. It also makes the object resistant
to change or fluctuate on its own [2].
Similar to cells in
cellular automaton, the patterns and behaviors are
created through each step of evolution through space and
time. These cells are updated based on the state of
neighboring cells that progressively update in space
and time. In class IV of cellular automata, information
for change of behavior is carried over a long range [7].
Any change with its behavior is emerged without any way
to reduce this information. Because of this long range
of information communicated between structures or
patterns being produced, cohesion has established a
unity property for overall structure that inevitability
makes the information irreducible.
The irreducibility of cohesive properties has
implication for other areas of science such as biology.
In biology, the organisms are cohesive with their
structural and functional connections that make them
unaffected to the continuing change in their composition
and even their form [2]. For example, the “broken wing”
behaviors of some birds in the presence of predators
might seem to be a coherent deception to protect
offspring [2]. Then after the distractions succeed, the
bird will take an alternative route back to its baby
birds.


a) Killdeer
b)
Thick Knee
Figure
1. Killdeer and Thick Knee Distracting Predator
a)
Killdeer and b) Thick Knee are displaying broken-wing
behavior when they sense a predator to protect their
offspring. They act pitifully to distract the predator
when it approaches baby birds. The broken-wing makes the
predator follow them while keeping themselves one-step
away from predator. Once when the predator is off range
from baby birds, the broken-wing behavior suddenly heals
and they fly away. [8] [9]
This cohesive behavior
appeared in many systems in our universe whether it is a
biological process, mathematics, physics or even a
general matter in our every day life. In many respect,
scientists favor mathematics formulas or physics laws to
explain some of these phenomena. Conceivably,
irreducibility can also exist in basic mathematics or
physics.
3.2 Computational
Irreducibility
In retrospect, many scientific experiments are practiced
to simulate promising model or framework for solutions
that will solve other similar problems. However, these
models usually solve for one particular problem but not
on other similar problems. There are numbers of
fundamental mathematics where irreducibility emerged in
number theories. Scientists use formulas to explain
complicated solutions in a simpler term, though some of
these terms are merely a symbol to another extrapolation
for what really ought to be known. For instance,
comparing rational and irrational numbers such as a base
10 rational number of the form p/q always reveals
a sequence of repetition in the decimals place. On the
contrary, irrational numbers such as √3 generate a
seemingly random sequence [7]. Consider the following:
|
1/13 =
0.076923076923076923… (Geometric Series)
√3 =
1.7320508075688772935… (Random Sequence of Decimal
Digits)
π =
3.141592653589793238462643383279502884197169399375105820974944592
30781640628620899862803482534211706798214808651328230664709384460955
05822317253594081848111745028410270193852110555964462294895493038196
… (The exact
value remains mystery) |
When dividing 1 by 13, it
generates a sequence of ‘076923’ as the repetition for
decimal portion known as geometric series. Since 13 is a
divisor of 999999 with a quotient of 76923, it is safe
to predict its repeating region without using a high
precision calculator. For irrational numbers, √3
generates a seemingly random sequence of
‘7320508075688772935…’ with continually growing digits.
This sequence is computationally irreducible with any
form of mathematical shortcut. It will take endless
pages to write down digits to represent the actual
sequence of √3. As a result, mathematicians prefer to
present answer in the form of ‘√3.’ Similar to the
representation of π first discovered back in 1600s, a
complete value of π remains mystery. Despite the simple
definition of π as the ratio of the circumference to the
diameter of a circle, its sequence is considered
sufficiently random.
Can a similar phenomena exhibit in cellular automata
models? When experimenting with 1D cellular automaton
rules 98111117, 91111177, 93111117, 91151117, different
kinds of behavior in constant, repetition, seemingly
random, and localized structures are produced
respectively.


a) Code
98111117 (Class I)
b) Code 91111177 (Class II)

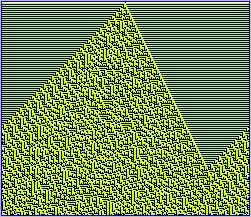
c) Code
93111117 (Class III)
d)
Code 91151117 (Class IV)
Figure
2. 3-State 1D CA with 4 Classes
CA
examples that showed in a) constant pattern b)
repetitive pattern c) seemingly random looking pattern
and d) seemingly random yet with some localized
structures patterns.
While the first two
systems on the top seemed to be computationally
reducible, the behavior of the third and fourth systems
appeared computationally irreducible. Indeed, whenever
there is computational irreducibility existing in a
given system, there is no way to predict the overall
system behavior without going through every step of
computation for the system itself [7]. Consequently, to
reduce the amount of computations will require building
another system with an equally difficult computational
process for such special rules to exist. After all, the
system itself needs to track all possible variables
emerged. In the end, it does not help to reduce much of
the computation but instead going through every single
step of evolution. In many biological processes seen in
nature, the growth development of a butterfly starts
from eggs, caterpillar, cocoon, and adulthood. It will
never skip intermediate development process. It goes
through various stages of evolution before a newly
emerged adult butterfly. Is it possible to make a
reduction of overall growth cycle from caterpillar to
butterfly directly? This coherent biological process
does not allow such reduction to take place in nature.
This led to the notion that information or process for
many systems in nature is always increasing and highly
dependent onto their causal relationship.
3.3 Entropy Increase
Entropy has led to the
notion of irreducibility to some systems in nature.
Entropy seems to increase over time as more information
tends to be generated in any given system. This concept
is known as Second of Law of Thermodynamic. A specific
measurement for any entropy will depend on the system
itself and future processes it generates [7]. For
example, a cellular automaton that is setup with simple
rules might generate behaviors of plain pattern
initially; as evolutions progresses, a more chaotic
behavior seemed to emerge. The behavior of seemingly
random patterns has carried information that
communicates with future evolution over long range. The
patterns do not seem to die out nor conform to any
regularity. Instead, the behavior of such patterns
emerges as evolutions continue. To reduce the amount of
computations and discover the final behavior is
implausible.


a) Simple
Repetitive Pattern
b) Random Looking Pattern
Figure
3. 3-State 1D CA Random Pattern
CA
example using Code 39833579 showed a) simple repetitive
pattern in the first hundred of evolution, b) after
about 200 steps when patterns are overlapping each
other, a seemingly random pattern emerged.
When entropy is exhibited in a system, reducing its
computation is nearly impossible. The Second Law of
thermodynamics inferred if one repeats the same
measurements at different times, then the entropy
deduced from the system would tend to increase over time
[7]. Just as how it appears in nature, behaviors emerged
can be highly complex without a systematic way to reduce
its overall pattern of behavior. Do patterns of these CA
examples truly show complexity that cannot be perceived
by human intuition, or is it merely a perception that
cannot be accepted by human intellectual capacity. For
the most part, patterns generated with this level of
complexity undoubtedly cannot be captured with normal
human perception. Even with a high-speed super computing
device, it computes this information exhaustively
without knowing what patterns or behaviors come next.
With the amount of irreducible information increasing
over time, the probability of getting accurate
prediction over future behavior is diminishing.
4 Unpredictability
4.1 Defining
Randomness
Contradicting to what
many believed that Second Law of Thermodynamics explains
universality in the physical world, Wolfram has used the
example of reversible cellular automaton with rule 37R
to demonstrate a seemingly random behavior that cannot
be predicted with this law. The Second Law of
Thermodynamics dictates randomness and entropy will
always increase after its initial condition. Conversely,
patterns generated by rule 37R appear to fluctuate
between order and disorder states. As in consequence,
rule 37R does not follow prediction of Second Law of
Thermodynamics. Moreover, an unpredictable behavior such
as rule 37R indeed cannot be predicted with any form of
mathematic formula or physics laws. To explain
universality, Wolfram argued that Second Law of
Thermodynamics is not universally valid even if it is an
important and quite general principle.

Figure
4. 2-State 1D CA rule 37R
An
example of CA that does not follow Second Law of
Thermodynamics. [5]
Defining what a true
randomness is could vary depending on how humans
perceive the system. Most intuitively, randomness is
described with system of behavior without apparent
regularity. According to Wolfram, rule 30 in elementary
1D cellular automaton shows a seemingly intrinsic
generation of randomness. Such randomness is believed to
be generated without any form of insertion or external
environmental effects. The intrinsic randomness is
essentially what makes Wolfram believed that a simple
underlying rule could still generate a behavior of great
complexity. In essence, the steps of evolutions are
determined, new states are created and updated through
space and time. Assuming our universe behaves as
cellular automata similar to rule 30, then each step of
history event is created intrinsically without anyway to
predict what future events will emerge. This history of
events has exhibited causal relationship one above and
one below its underlying system. However to skip
interconnected neighboring relationships for the cells
and leap to the very last stage of evolution is not
possible. If history of events are in fact created and
updated at each step through space and time, a notion of
unpredictability will emerge in nature. Viewing this
intricacy of overall history of causal connectivity
exemplify the perception of complexity.
4.2
Perception of Complexity
Complexity and
randomness are used interchangeably in the context of
our everyday experience. Complexity can also be viewed
as the level of perception from human intuition. For
example, class III and IV of cellular automata can be
perceived random, thus complex. However, it may well be
human perception that does not accept its appearance of
behavior at its base level. Given a cellular automaton
behavior with pattern analogous to class III in picture
a), it was merely a version of class II cellular
automaton with its initial condition randomized.


a) Random
Initial
Condition
b) One Cell as Initial Condition
Figure
5. 3-State 1D CA Complex Pattern
Rule Code
91111177 showed a) seemingly complex and random behavior
with randomized initial condition. b) Using the same
rule with its initial condition set to one cell.
A notion of unpredictability can even be seen when
describing the pattern from Code 9111177. In everyday
experience, human tend to interpret things with complex
behavior that must somewhat be created with rules of
great complexity. Moreover, our intuition also suggests
that if a pattern has no apparent regularity, it cannot
possibly be generated from a pattern that looks so
regular and repetitive. Likewise, in nature many
behaviors and processes are quite unpredictable at its
superficial level. Some behaviors may seem as complex as
in picture a) , but without
knowing its simpler case
in picture b), human might be leading into different
intuition of interpreting aspect of behavior in our
nature. This intuition can be either developed or innate
from human response; nevertheless, properties of nature
reflect uncertainty that cannot be easily understood
with human conception.
4.3
A Notion of Uncertainty
In the physical world,
the most evocative model can be best described with laws
of physics. These laws elaborate nature with use of
examples from particle physics, theory of relativity and
so on around our universe. One of the profound findings
in the history of physics was Uncertainty Principle
by Heisenberg. Heisenberg stated “uncertainty
relation between the position and the momentum (mass
times velocity) of a subatomic particle, such as an
electron. This relation has reflective implications for
such fundamental notions as causality and the
determination of the future behavior of an atomic
particle.” Why use particles to describe behavior of the
universe? Physicists believed using the smallest defined
and perceived unit could best mimic what is happening in
nature. To sum up Heisenberg’s uncertainty principle,
the more precisely the position of an object is
determined, the less precisely the momentum is known in
this instant, and vice versa. In another word, if we try
to measure some moving object in the universe, we cannot
both decide precisely what speed it is moving and what
position it locates. If we try to measure one of them,
we cannot measure the other [5].
By means of 1D cellular
automaton according to Wolfram, the edge of the pattern
produced by cellular automata rule has a maximum slope
equal to one cell per step. It is also considered the
absolute upper limit on the rate of information
transfer, similar to the speed of light in physics [7].
Imagine again that cellular automaton represents
universe with its history created through space and time
at each step of evolution without wrapping.
Theoretically, there should not be a precise way to
predict the next evolution if only one measurement of
speed or position can be captured but not both! With
this assumption, recall rule 30 in elementary 1D
cellular automaton. It tends to increase its randomness
and complexity if it were running at an edgeless space
in the universe. To a certain extent, it is
incomprehensible even with human perception and
analysis. Moreover, if precise measurement of either
speed or position of any matters in the universe is not
possible, the entire emergences we see in nature
inevitably exist without our knowledge. This led to the
notion of free will when any process and behavior emerge
in nature.
5
Determinism and Free Will
What defines free will in cellular automata? Free will
means there must be at least two or more possibilities
when facing a given choice. Free will also means no
coercion and choice is not forced. Many systems in our
nature generate behaviors that are random and complex.
The entropy and information tend to increase as time
elapsed with the amount of information that is
disordered. Computational irreducibility is the origin
of the apparent freedom of human [7]. If the evolution
of a system corresponds to an irreducible computation
then this means that the only way to work out how a
system will behave is essentially to perform this
computation. It is our perception that dictates how a
complex system eventually will lead to a computation
that seemed irreducible. It also suggests there can
fundamentally be no laws that allow one to work out the
behavior more directly [7]. A cellular automaton whose
behavior displays characteristic of computational
irreducibility could show an analog of free will. Even
though its underlying laws are definite and simple, the
behavior is complicated enough that in many respects
follow no definite laws [7]. This phenomenon appeared in
many disciplines of our universe. For instance,
behaviors and processes are evolving and changing
through space and time. Even so, human are evolving and
changing with their intellectual capacity over time.
When choices are present, evolutionary paths evolve
forever.

Figure
6. 2-State 1D CA
Rule Code
1599 showed the patterns follow no definite laws. Most
patterns and structures seem emerged without any way to
predict. The only possible way to analyze this rule is
to run through the whole computation.
Insofar, many of these
existing behaviors were based on human assumption,
perception, and analysis as an insider point of view
since we are ourselves part of this universe. Instead of
running our universe as what has been described as
cellular automata, we are merely exploring a part of
this universe where the complete history exists. What
would it be like? From an observer’s perspective, if the
universe is modeled as a Multiway System given a set of
simple rules, multiple histories at any given step of
evolution seem to emerge [7]. Each history created could
escort in different paths from each other. Taking one
slice of the Multiway System, another history
perspective is being perceived by an observer. What
happened if our universe is operating in the way where
multiple histories are created and updated synchronously
or even asynchronously? The degree of this indeterminism
might trigger why these properties such as
irreducibility and unpredictability exist in nature.
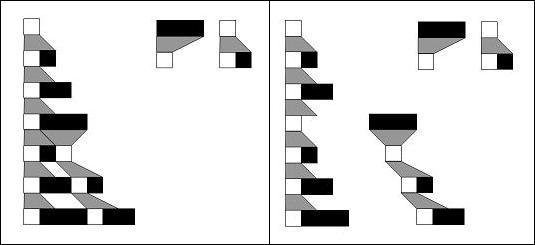
a)
Universe with unique history b)
Universe with multiple histories
Figure
7. Universe illustrated with Multiway System
As an
observer perspective, there might be multiple histories
created in our universe. Using a set of simple rules, a)
a universe with more than one choice to update at each
evolution. b) If slicing what has been created in the
universe, multiple histories seem to emerge.
6 Conclusions
The concept of emergence
consists of irreducibility and unpredictability
properties that prevent scientists from concluding
certain findings. These properties appeared in many
areas of our everyday experience. For instance, in
mathematics, physics, or even in biological behaviors.
Scientists in various fields are constantly looking for
better models to describe this ever-changing universe.
During this endless research, new methods or findings
were discovered, in many instances with the notion of
the emergence emerged in nature. If scientists do not
perceive this emergence existed in systems that create
randomness and complexity, subsequently it does not
raise much of an attention or interest to their
discovery. Correspondingly, Heisenberg stated, “we only
observe what we can observe, if anything that we cannot
be observer, it is equally not observable.” Cellular
automaton is certainly one of the most descriptive
emergent computing models that help us to begin our
science exploration. We can analyze some of these
concepts emerged in emergent computing where
irreducibility and unpredictability exist. Consequently,
irreducibility and unpredictability prevented us from
perceiving and analyzing models that conclude our
nature.
References
[1]
Klaus A. Brunner, What's Emergent in Emergent
Computing? 2002.
http://winf.at/~klaus/emcsr2002.pdf
[2]
John D. Collier and Scott J. Muller The Dynamical
Basis of Emergence in Natural Hierarchies, George
Farre and Tarko Oksala (eds) Emergence, Complexity,
Hierarchy and Organization, and Selected and Edited
Papers from ECHOS III Conference, 1998.
[3]
John D. Collier, Causation is the transfer of
information; Causation of Law and Nature, (ed,
Howard Sanky) Kluwer, 1998.
[4]
Claus Emmeche et al. Levels, Emergence, and Three
Versions of Downward Causation. In: Peter Bogh
Andersen et al.(eds.), Downward Causation: Minds, Bodies
and Matter. Aarhus University Press, 2000.
[5]
Werner, Heisenberg History Museum, 1976
http://www.aip.org/history/heisenberg/p08a.htm
[6]
Timothy O’Conner, Emergent Property. 2002
http://plato.stanford.edu/entries/properties-emergent/
[7]
Stephen Wolfram, A New Kind of Science, Wolfram
Media, Champaign, IL 2002, p 138, 140, p 518, p 301, p
737-750, p750, 752, 967, 1132, 1135
[8] Outdoor Photographing.
Killdeer Photo Source:
http://www.outdoorphoto.com/birdtips.htm
http://www.holoweb.com/cannon/killdeer.htm
http://home.eol.ca/~birder/plovers/kl.html
[9] TrekEarth. Thick Knee
Photo Source:
http://www.trekearth.com/gallery/South_America/photo1197.htm
Presentation Slides
|