Traffic
Flow with Cellular Automata
Table of Content
Abstract: 2
Introduction: 2
NS Model: 2
FI Model: 3
The Basic Model: 3
Vehicle Movement: 3
Benyoussef’s Simulation: 4
Vmax = 1: 4
Vmax = 2: 5
The Two-Lane Model: 6
Traditional Lane Changing Rules: 7
NS Lane Changing Rules: 7
The Simulation: 8
Additional Reality-check Rules: 9
Result and Discussion: 11
One Lane Model: 11
Two Lane Model: 12
Reference: 12
Abstract:
Cellular automata has been recently use in many scientific
calculations and simulations.
In this paper, we will discover how cellular automata can be
applied to traffic flow simulations. The cellular automata simulation is driven
according to a set of local rules, which are defined as the local relationships
between itself (the center cell) and the neighboring cells.
Traffic problem is a major problem in most of the major cities
in the United States, as well as other major cities around the world. The need
to accurately and realistically predict traffic flow is expanding. There has
been recently much of interest in studying traffic flow with Cellular Automata
models. Why CAs? CA models are conceptually simple, thus we can use a set of
simple CA rules to produce complex behavior.
Through the use of powerful computers, these models can encapsulate the
complexity of the real
world traffic behavior and produces clear physical patterns
that are similar to those we see in everyday life. For example, CA models show
the shifting from moving traffic to jamming traffic.
The basic one-dimensional Cellular Automata model for
highway traffic flow is the CA rule 1841. Cay Horstmann2,
a professor at SJSU wrote an interesting Java Applet to simulate traffic flow
with a 1-D CA based on Kai Nagel and Michael Schreckenberg3 (NS)
rules. The NS model is a variation of rule 184, which is one of the elementary CA rules investigated by Wolfram. The
model describes a one-lane traffic road with sequence of grid points, and each
grid point is a square representing one vehicle. There are many variations on the basic model. The NS model
considered the effects of acceleration and delay of vehicles with high speed.
The actual speed of the car at each time step depends on the “lambda” value
that can be adjusted accordingly. This
model captures the realistic traffic situations where the car accelerates and decelerates.
Fukui and Ishibashi (FI)4 introduced yet
another variation on the basic 1 D CA model, which generalizes the cellular
automata rule 184. The FI models considered that cars could move by at most vmax sites in one time
step if cars in front do not block them. More precisely, if the number of empty
sites in front of a car is larger than vmax at time, then it can move forward at most vmax sites in the next
time step with probability (1 inv f). Here, the probability f represents the degree of stochastic delay. The FI model differs from
the NS model in that the increase in speed is instantaneous, and depends on vmax. In general, the stochastic delay only
applies to slower car since they do not slow down for the reason that they are
already slow. The two models are
identical for vmax = 1, vmax = 1 basically means the vehicles can only move 0 or 1
sites at each time step.
These simple models have been shown to reproduce at least
qualitatively the features of real traffic flow. As we have seen in the above
models, the basic idea is to formulate a model in space and time. The space in
this case is the road divided into grid points or cells that may be empty or
occupied by exactly one vehicle.
The
FI4, a variation of the basic model, differs from the NS5
in that the increase in speed may not be gradual and stochastic delay only
applies to high-speed cars. Therefore, the definition of Space Gap here only
applies to the FI model. In the FI model, the vehicles can advance by at most M
sites each time step if they are not block by vehicles in front. If M = 1, then
the FI and NS is identical. Therefore we will be referring to the FI model from
now on.
The model contains three parameters: the maximum speed Vmax
which is same for all the vehicles, the probability of cars arriving onto the
road, and the probability of some cars on the road slowing down. The following
paragraphs will explain how the vehicles move according to the rules.
Defined
Space Gap as “the distance between successive vehicles in the traffic lane
measured from a common reference point on the vehicles, in the case, any parts
from the vehicle can be use as a reference point.” The optimal space gap is therefore the smallest gap between two
vehicles without causing an accident. If all the vehicles maintain the optimal
space gap, then the density of the road is maximized. As one suspects, the space gap has a direct relationship with the
speed of the vehicles.
This
model considered the fact that not all drivers adhere to the legal speed limit,
and therefore a fraction of the vehicles accelerates. Similarly, some drivers
may choose to decelerate without a reasonable cause. Combining the two factors,
we can develop a relationship between accelerating, decelerating, and
maintaining constant speed.
· Pkeep -
Probability of maintaining speed
· Pacc -
Probability of increasing speed/accelerating
· Pbreak -
Probability of decreasing speed/decelerating
A
random number Î[0,1]
is used to decide whether a vehicle will decelerate to the legal speed,
maintain constant speed, or accelerate to the maximum speed (maximum speed is
user-defined). The user may specify the probabilities of accelerating and
decelerating and maintain constant, however, these probabilities should add up
to 1. At each time step of the simulation, a random number is generated for
each of the probability as follows:
If
random number x < Pkeep , keep
constant speed at current time step.
Else
if x < Pbreak, vehicle should break.
Else
vehicle should accelerate.
The
probability of decelerating deserves some explanation since breaking is totally
legitimate in certain situations. The drivers who are driving with unsafe space
gap may choose to break to achieve optimal space gap.
The
average occupation of each cell (vehicles on the lane), the average velocity
and the flow of vehicles are all depended on the space gap mentioned above.
Benyoussef4 discussed the time evolution of these dependants using
the time evolution of the dynamical equations with the mean field approximation
(MFA) and using numerical simulations. Benyoussef’s simulation setup is
basically the same as Hortsmann’s applet simulation where during each updating procedure, the new cars positions
do not influence the rest and only previous positions have to be taken into
account. Benyoussef’s simulation obtains the average occupation, average
velocity, and the flow by averaging the velocities and currents over 21 cells.
The
simulation studies Vmax = 1 and Vmax = 2. In the case of Vmax = 1, the
simulation takes a different turn from the traditional simulation methods.
Instead of using density as “order parameter” [4, pg. 6], it uses the average
velocity calculated above to determine three phases of traffic flow: traffic
jamming phase, moving phase, and maximal flow phase. The moving phase
corresponds to low vehicle density while the jamming phase refers to high
vehicle density. The three phases
exhibit two transitions; the first order transition is formed by the moving
phase to the jamming phase and vice versa; the second order transition is
formed from the moving or jamming phase to the maximal flow phase and vice
versa. If the desired traffic flow is the moving phase, then inject fewer
vehicles onto the road. If the desired traffic flow is the jamming phase, then
inject vehicles to make the road denser. The interesting phase is the maximal
flow phase, which is achieved by finding equilibrium point between the entering
and exiting rates and the average velocity of the vehicles. The phase diagram from
the simulation shows that by increasing the braking probability p, the
equilibrium point is always at ½ entering and ½ exiting as shown on figure
3. On the other hand, the braking
probability “arises only as a factor in
the dynamical evolution of the MFA equations” [4, pg.6], and it only affects the time required to reach the steady
state.
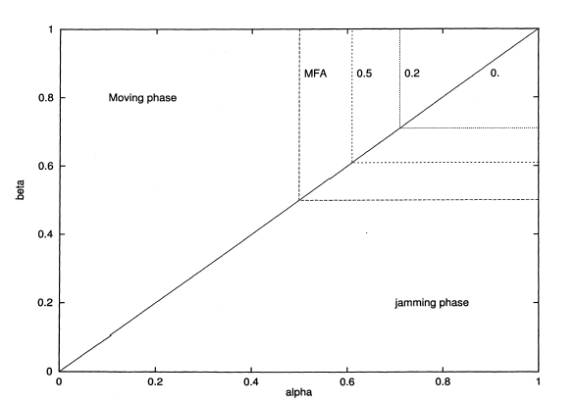
FIG. 2. Phase diagram (entering rate; exiting rate) in the case vmax = 1, obtained from MFA (continuous line) and
simulations (dashed line) for different values of p indicated in the figures.
In
the case of Vmax = 2, the vehicle can move one or two sites during
each time step provided the two sites ahead are empty; otherwise, it can move
only one site or remain constant. In
contrast to Vmax = 1, the braking probability plays a major role in
determining the steady state. Using the comparison between the MFA equation and
Benyoussef’s simulation, increasing braking probability allows the number of
vehicles entering the road exceeds the number of vehicles exiting it. And as a
result, the equilibrium between the entering rate and exiting rate is
destroyed. The maximal flow phase, therefore, is no longer at ½ = ½. Instead,
the maximal flow phase occurs at ½ entering = 1/3 exiting as shown
on figure 4.
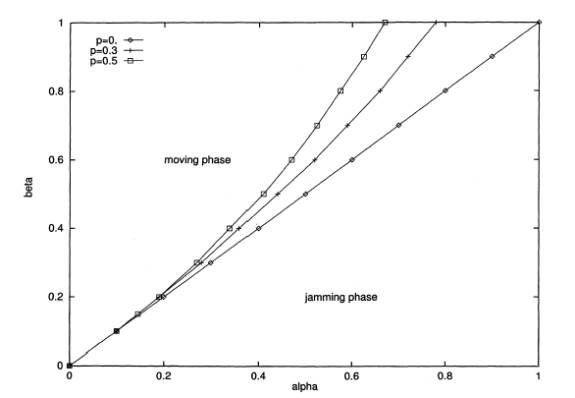
FIG. 4. Phase diagram (entering rate; exiting rate)
in the case vmax = 2, for different values of p.
The
basic model does not mention rules for switching lanes despite its idealism in
modeling real traffic flow. Realistically, we would need some rules for changing
lanes; we can do this by adding addition rules to the above. There are several
factors that will determine the rules, these include local vehicle density,
vehicle distribution, but will ignore local road topology. This model includes
both deterministic and random components.
The
deterministic component of lane changing is based on the above rules for the
movement of the vehicles in a one-lane road. Instead of looking at just one
lane, now the model considers the behaviors of vehicles in a two-lane road. The
vehicle will change lanes if the traffic conditions are better on either of the
neighboring lanes.
Much
of the work done in the past by individuals, government agencies, or private
institutes have been concentrated on the basic 1 D CA model, we’ve only
discussed the basic 1 D CA model thus far. The attention now is to focus on the
two-lane CA model by Kai Nagel ET EL5. The idea proposed in this model is to look for systematical
structures in the rule sets for lane changing.
The traditional two-lane model uses the microscopic model by
Wiedemann6. Following Wiedemann’s model, Sparmann7
distinguishes between the wish to change lanes at any given time and the
decision to change lanes. Imagine a lane change from the right to left,
a wish to change lane is a result of another vehicle ahead obstructing,
and a decision to change lane is the action of changing lane if there’s
enough space in the other lane. On the
other hand, if the vehicle is changing lane from left to right, then a wish to
change lanes is if in both lanes there is nothing ahead obstructing. The term
obstructing is defined to be psychophysiological thresholds. What this means is
that there are three outcomes: no obstruction, light obstruction, and heavy
obstruction, depending on the speed difference and distance.
In
practice, the Wiedemann model uses a time discrete formulation of differential
equation. But with the increasing “popularity” of using cellular automata to
simulate differential equations, M. Cremer8 and co-workers
implemented cellular automata lane changing rules. Following Sparmann, they set
the rules as follows:
“Lanes are changed
to the left if a slower vehicle is less than ll cells ahead and if a
gap of size Dx exists on the left lane; lanes are changed to the right if, in the
right lane, there is no slower vehicle less than lr cells ahead and there is a gap of size Dx in the right
lane.” [5, pg. 3]
By
looking at Sparmann’s suggestion on lane changing, one can see that the density
inversion of lane usage. Yet, nobody has included this detail in their
research. The NS model stressed the
importance of density inversion of lane usage.
The NS two-lane model first considers “Security”. Security
in a sense is very much like the Space Gap discussed above, it means that one
leaves enough space in front and behind oneself. Security is easily enforced as long as one stays in a single-lane
road. In the case of two lanes, changing lanes means that there must be enough
space in front and behind the target lane. This may not be so obvious in some
cases. For example, a compact vehicle may have different security standard with
an eighteen-wheeler truck. Let’s defined Security Gap to be the gap between
boundaries [-Vmax, v], v = current vehicle
velocity that wants to change lane, Vmax = maximum velocity
of vehicles allowed. In summary, a lane is changed if the security gap is
fulfilled and if there’s a good reason to change lanes. The second fulfillment
exactly described in Sparmann’s wish and decision.
In
analyzing the rules for changing lanes, we need to understand that the driving
behaviors vary in different countries. For example, in hypothetical Germany
freeways, passing is not allowed on the right. This means that if a vehicle is
on the right lane, it can change to left if there is a slow vehicle on the same
lane or in the left (vr<v.OR.vl<v). The vehicle changes back to the
right lane as soon as the velocities of cars on both lanes are sufficiently
large (vr>v AND vl>v). In hypothetical
American freeways, passing on the right lane is allowed, however in practice,
it rarely happens due to the nature that slower vehicles merge on to the
freeway from the right. The vehicle changes back if there is a faster car on
the right (or none at all). This driving behavior characterizes the asymmetric
(also known as the German) lane changing rules, which is used in NS’s paper.
As we have mentioned above, the advantage of using powerful
computer to implement a set of simple rules (cellular automata) immediately
takes effect in this model. The lane changing algorithm implemented is as
follows:
“In even time steps, perform lane changes from the
right to the left. All vehicles in the right lane for which the incentive
criterion (vr<v.OR.vl<v) and the security criterion ([-vmax ,v]) are fulfilled are simultaneously moved to
the left. In odd time steps, perform lane changes from left to right.
All vehicles in the left lane for which the incentive criterion (vr>v AND vl>v) and the security criterion
([-vmax ,v]) are fulfilled are simultaneously moved to
the right.” [5, pg. 4]
There’s also a very critical factor not
mentioned in the above rule. The number of sites one looks ahead can’t be too
close and can’t be too far. If one looks too close, one does not see close
ahead vehicles and therefore will brake with a high probability. If one looks
too far, “one has a tendency to go to the left lane already far away from the
obstructing vehicle, thus leading a strong density inversion at low densities.”
[5, pg. 4]
The author of this simulation decided to look
ahead at most 16 sites and suggested that this look ahead parameter can be
adjusted to density inversion.
The rules for vehicle movements are taken
straightforward from NS’s one-lane model: If the velocity is lower than maximum
allowed, accelerate with a probability. Else if the velocity is greater than
the security gap, then slow down to avoid accidents. Else with a certain
probability, slow down the vehicle for no good reason. These rules generate
reasonable relationships between velocity, density, and flow. One important
discovery to note is that these rules generate the density inversion below
maximum flow.
After comparing the velocity-based (NS) and
gap-based (Wagner [5, pg. 4], one has a reason to change lane even there’s not
enough space) lane changing rules, a “slack” variable S is introduced to the NS
simulation. The problem with
velocity-base rules is that the maximum inversion is reached at a very low density.
This problem can be fix easily if one incorporates a slack value S into the
rules similar to the one in the gap-based rules in addition to the look ahead.
In doing so, the look ahead distance is reduced to obtain realistic lane usage. Nevertheless, it also introduced the side
effect that traffic never reverts to an equal lane usage. To overcome this side effect, the simulation
considers vehicles with zero speed attempts to change lane when the speed on
the other lane is higher than in its own lane (“symmetrization”).
Although maximum inversion is achieved, it is
unclear how to account for the presence of slower vehicles such as trucks. As
we have mentioned before, the security gap should be different for vehicles of
different size in reality. NS’s two-lane model follows Wieldmann’s data, which
includes 10% trucks, by giving 10% of the vehicles a lower maximum velocity and
keeping the same acceleration capabilities for all vehicles. The result from
adding the above rules to the model is that the maximum flow shifts toward
higher densities.
With the addition of the slack variable and
10% slower vehicles, the NS two-lane simulation result sets are now closer to
reality. As one studies the result sets, one will see that traffic with slow
vehicles is different from traffic without slow vehicles. In investigating
whether flow breakdown is related to a single-lane breakdown in the left lane,
this model simulates traffic with slow vehicles and traffic without slow
vehicles separately.
In the case of traffic flow with the absence
of slow vehicles, the lane usage at maximum flow for one-lane and two-lane is
not much of the difference using the “basic” velocity-based rules.
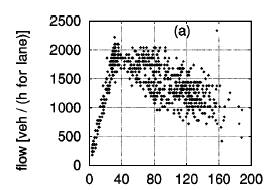
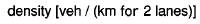
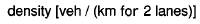
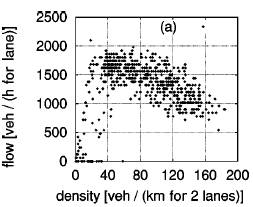
The
Fundamental Diagram (a) shows density vs. flow plot for the single-lane rules,
in two independent lanes. Fundamental Diagram (b) shows the left lane of basic
velocity-based lane changing rules. And Diagram (c) is the plot for the right
lane of basic velocity-based lane changing rules. The Fundamental Diagrams are
in perfect compliance with the claim that lane usage is not much of the
difference; the points near maximum flow are almost the same. Diagram (b) shows
the left lane, which is the same as the right lane in (c). So one might suspect
that flow breakdown is independent. As it turns out, left lane reaches maximum
flow earlier than right lane and from then on all the additional incoming
density is position to the right lane. When the combined density of both lanes
is higher than the maximum flow density, flow breakdown occurs.
When
slow vehicles are included in the simulation, the two-lane situation behaves
more like the one-lane situation than the two-lane situation without slow
vehicles. This suggests that the presence of slow vehicles is more critical in
analyzing traffic flow than the difference between one-lane and two-lane. Realistic situations reinforced this
suggestion; fast vehicles jam up behind a slow vehicle and create the stop-and-go,
go-and-stop dynamic. Two slow vehicles moving side by side, disallowing any
form of lane changing create the stop-and-go dynamic in the two-lane situation.
The basic velocity-based lane changing rules shows the vehicles on both
“jamming” lanes have similar length. On the other hand, the additional slack
and “symmetrization” rules, there are more vehicles on the left lane than on
the right lane.
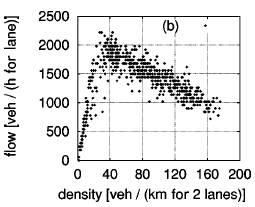
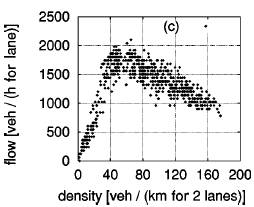
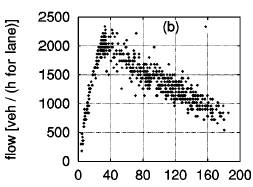
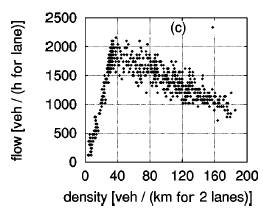
The
same Fundamental Diagrams with slow vehicles, indicates that the maximum flow
points don’t have a lot in common. In (b) and (c), the points look promising,
however, the points near maximum flow are higher in (b) the left lane than in
(c) the right lane. The flow in the left lane is higher than the right lane and
the one-lane traffic flow. Unlike before, the flow breakdown is cause by the
slow vehicles on both lanes.
In this paper, we have studied models based on the NS
models with the maximal acceleration vmax (FI models). We have seen simulations using
probabilities to determine the movement of the vehicles. We also have seen cars
could enter the road with an entering
rate (1 inv p) probability and removed from it with an exiting rate (1 inv p) probability.
This kind of system exhibits three phases for vmax = 1, a moving phase, a jamming phase and the maximal flow
phase. The transition from one phase to another is affected by the entering
rate and exiting rate, and the average velocity. The maximum flow phase occurs
at 50% entering rate = 50% exiting rate with high average velocity. When vmax = 2, the
maximum flow phase does not occur at 50% = 50%. The system only exhibits first
order transition due to lost of the equilibrium point.
The author of this paper have also set up a
different set of rules to simulate traffic flow following the same idea of the
basic model. Instead of using probabilities to determine the movement of the
vehicles, the simulation uses a set of preset rules. The preset rules take the
current vehicle as the center cell and look at its neighbors in a one-lane
road. The speed of the current vehicle is therefore predicted by its neighbors.
For low density, the simulation exhibits maximum flow even if vmax =
2. This kind of behavior is a class III classification in Wolfram’s
book “A New Kind Of Science”, which is completely random behavior. For high
density, the simulation exhibits almost class IV behaviors, that traffic flow
repeats itself on some part of the road after certain number of steps while
other parts of the road exhibits random behavior such as jamming phase or
maximum flow phase.
The NS two-lane model introduces lane
changing rules while using the same one-lane vehicle movements. The rules were
broken into two parts, the first part uses Sparmann’s notion of wish and decision and
the security gaps to determine lane changing. Second, there’s the security
criterion which seems to be universal for all reasonable lane changing rules.
The exact value for the security gap doesn’t seem to matter much as long as
it’s sufficiently large. So the rules
simply means “change to the left when
either in your lane or in the left lane somebody is obstructing you” and
“change back when this is no longer true.’’ [5, pg. 12] Since applying the
above rules will introduce generic density inversion at high density, the
simulation adds “symmetrization” to the rules. And both the velocity-based and
gap-based model with slow or without slow vehicles give satisfying result.
[1]
Steven Wolfram, A New Kind of Science, (Wolfram
Media, Inc.) page 56.
[2]
Cay Horstmann, Traffic Simulator Applet, http://www.horstmann.com/applets/RoadApplet/RoadApplet.html.
[3]
M. Blue, B.W. Bush, Information content in the Nagel-Schreckenberg
cellular automata traffic model, PDF
file, http://public.lanl.gov/bwb/Information%20content%20in%20the%20Nagel-Schreckenberg%20cellular%20automata%20traffic%20model.pdf
Abstract:
estimate the set dimension and find bounds for the set
entropy of a cellular automata model for single lane
traffic.
[4]
A. Benyoussef et al., Traffic Flow in a 1 D Cellular Automata Model with
Open Boundaries, (Chinese Journal of Physics, Vol. 39, NO. 5, October
2001), PDF file, http://psroc.phys.ntu.edu.tw/cjp/v39/428.pdf
Abstract:
focuses on the effect of breaking probability and a
maximum velocity on the density, flow and average velocity
of cars moving in the middle of the road.
[5]
Kai Nagel et al., Two-lane traffic rules for cellular automata: A systematic
approach,(Physical Review E, Vol. 58 No. 2, Aug. 1998), PDF file, http://www.sim.inf.ethz.ch/papers/nagel-etc-2lane/nagel-etc-2lane.pdf
Abstract:
summarize different approaches to lane changing and
the results and propose a general scheme, according
to which realistic lane changing rules can be developed;
test this scheme by applying it to several lane changing
rules, which, in spite of their differences, generate
similar and realistic results.
[6]
R. Wiedemann, Schriftenreihe Heft 8, Institute
for Transportation Science, University of Karlsruhe,
Karlsruhe (unpublished)
[7] U. Sparmann, Spurwechselvorga¨nge auf Zweispurigen
BAB–Richtungsfahrbahnen, No. 263 in Forschung
Straßenbau und Straßenverkehrstechnik (Bundesminister
fu¨r Verkehr, Bonn–Bad Godesberg, 1978)
[8] M. Cremer and J. Ludwig, Math. Computer
Simulation 28, 297 (1986).